Mediation and instrumental variable analysis

Mediation analysis

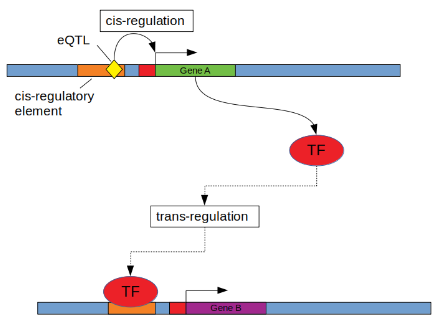
Figure by Sean Bankier from this review.

The GTEx study identified trans-eQTLs that are also cis-eQTLs and asked if the cis-eGene could be the cause of the trans-eQTL association (see fig above), that is, if the following model is supported by the data:

flowchart LR
  Z --> X --> Y

where \(Z\) is a SNP that is a cis-eQTL for gene \(X\) and trans-eQTL for gene \(Y\). This model implies that \(X\) blocks the path between \(Z\) and \(Y\), and hence that \(Z\) and \(Y\) are independent conditional on \(X\), in mathematical notation

\[ Z \perp Y \mid X \]

The principle for testing whether the model \(Z\to X \to Y\) is true using the conditional independence criterion is illustrated in the figure below. Assuming linear relations between all variables, three conditions must be met:

The expression levels of \(X\) differ significantly between the genotype groups of \(Z\) (to confirm the \(Z\to X\) association).
The expression levels of \(Y\) differ significantly between the genotype groups of \(Z\) (to confirm the \(Z\to Y\) association).
The residuals of \(Y\) after regression on \(X\) do not differ differ significantly between the genotype groups of \(Z\) (to confirm that the \(Z\to Y\) association is mediated by \(X\), and hence that \(Z\to X \to Y\) is true).

Instrumental variable analysis / Mendelian randomization

The mediation method fails if \(X\) and \(Y\) are affected by common cause \(U\) (which may be an unknown or hidden variable):

flowchart LR
  Z --> X --> Y
  U --> X & Y

In this case, conditioning on \(X\) opens the collider \(Z \to X \leftarrow U\), creating a path \(Z\\; --- \\; U \to Y\), such that the residuals of \(Y\) will still show a difference between the genotype groups of \(Z\), and the mediation method concludes (wrongly!) that the \(Z\to Y\) association must be due to another factor than \(X\) (no causal \(X\to Y\) relation).

Instrumental variable, known as Mendelian randomization (MR), is an alternative causal inference approach that is not affected by hidden confounders \(U\), but with subtly different underlying assumptions.

Specifically, in MR we assume that the \(Z\to Y\) association must be due to \(X\) (for instance because \(X\) is the only cis-eGene of \(Z\), and trans-eQTL associations must be mediated by some initial cis effects), and we seek to estimate the magnitude of the causal effect of \(X\) on \(Y\).

The diagram above can be written as a structural equation model

\[ \begin{aligned} X &= a Z + c_X U + E_X\\ Y &= b X + c_Y U + E_Y \end{aligned} \]

where \(E_X\) and \(E_Y\) are error terms, mutually independent and independent of \(Z\) and \(U\). Since \(Z\) and \(U\) are assumed to be independent (no arrows in the diagram), it follows that

\[ \begin{aligned} \mathrm{cov}(Y,Z) &= b\\ \mathrm{cov}(X,Z) &= ab \end{aligned} \]

and hence the causal effect of \(X\) on \(Y\) is estimated by the ratio of covariances:

\[ b = \frac{\mathrm{cov}(Y,Z)}{\mathrm{cov}(X,Z)} \]